dBのよいところ【ミックスマスタリング学園】

オーディオを扱う際に私達は「dB」という言葉を使って音量を表現します。しかし、工学系の人間以外にとってこのdBという表現はあまり馴染みがなく、もしかしたら%や割という言葉で表現する方が最初はイメージしやすいかもしれません。

ではなぜdBを使うのか。それは、dBを使った方が直感的に音量を捉えることができるからです。そもそもdBとは何者なのかを振り返ってみましょう。

dBはある意味において%と似た性質を持っていてある信号に対して他の信号がどの程度大きいまたは小さいのかの比率を表すものです。こっちの信号はあっちの信号より**dB大きい/小さいといった言い方をします。

さて、ある信号の音量を変えることを考えてみます。%の場合何もしなければ100%です。音量を大きくすればこの100%よりも大きくなり、小さくすれば100%を下回ります。完全に消え去ると0%になります。

dBではどうでしょうか。元の音量は0dBで、音量が大きくなると正の値に、小さくなると負の値をとるようになります。信号が完全に消えると-∞ dBになります。

%を使って100% > 95% > 90% > 85% >…と5ポイントずつ下げていくと、音量は等間隔に小さくなっていきそうに見えますが、実際はそうはなりません。人間の感覚と照らし合わせると、最初のうちはほとんど変わらないのに0%付近では急に音量が小さくなります。

一方でdBを使って0dB > -5dB > -10dB > -15dB >…と5dBずつ下げていくと、音量は%の時と比べると比較的等間隔で下がっていくように感じられます。このように、dBはある程度人間の間隔に沿っているため音量の尺度として%よりも適していると言えます。

ではなぜdBの方が人間の感覚に近く感じられるかというと、人間の聴覚は音量差に対して対数的に反応すると言われているからです。対数的であるということは、ある信号の音量が2倍になること、2倍から4倍になること、4倍から8倍になること、32768倍から65536倍になることが全て同じ意味だということです。信号を「何倍にしたか」のみが感覚に影響し、例えば元の信号の音圧が何パスカルだったかは加味されません。（リニアな物理量の説明のために唐突にパスカルを出しましたが、デジタル信号処理の話の中に突然出すのは本アリはふさわしくありません。）

結局のところ数式を見るのが最も分かりやすいと思います。ある信号Aと別の信号Bの音量差をLとすると、Lは次の式でdBで表されます。

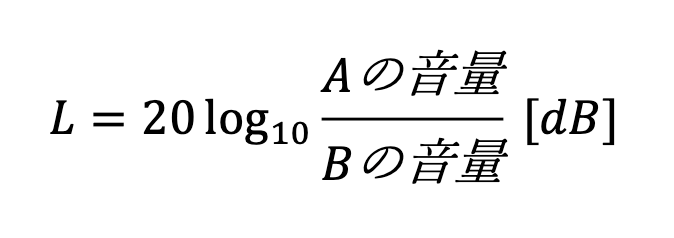
例えばLが約6.020dB下がることとAの音量が半分になること（もしくはBの音量が倍になること）は同義です。どんなに大きな音、小さな音でも、そこからの音量の変化を同じスケール感の数字で扱うことができるためdBは非常に便利なのです。

もしdBを使わず%で表現しようとすると、例えば小さい音を少しだけ大きくする時と大きな音を少しだけ小さくする時で異なるポイントを足し引きしなければなりません。10%の音を10%だけ大きくしたい場合1ポイント上げるだけで済みますが、90%の音を10%小さくするには9ポイント下げなければなりません。どれくらいの音量のものに対して変化を加えるかによって数値のスケールが変わってしまっては非常に不便ですよね。

dBを使わない場合、例えば24bitの整数のオーディオでは約1,600万段階の数値を扱わなければならず、信号の音量がそのどれくらいの段階にいるかによって数値を変更した際の音量感への影響もまちまちです。そんな膨大な領域においてもdBであれば一桁~二桁程度の数字で音量感を表現しきることができることも便利なポイントです。

長々と書いてきてしまいましたが、dBで音量を扱うことに慣れていけばいかにdBが音量を扱うことに適しているかを直感的に理解できるようになります。本記事の内容はその感覚的なdBの扱いやすさに対して辻褄を合わせる説明として、後から読み直してもらうだけで十分かもしれません。